Department of Physics, National Central University
Condensed Matter Physics Laboratory

Time-resolved reflectivity (TRR)
The TRR measurement is based on the fact that the index of refraction of a-Si is different with c-Si. With this difference, when the thickness of amorphous silicon changes, the net reflectivity will go through a cycle of constructive and destructive interference. Compare the theoretical reflectivity with the measured reflectivity, the depth of a/c interface can be calculated. Interference also enhances the sensitivity of the reflectivity measurement so that as little as 10~20 angstroms of interface motion can be detected, that makes a very precise measurements of the kinetics of the recrystallization possible.
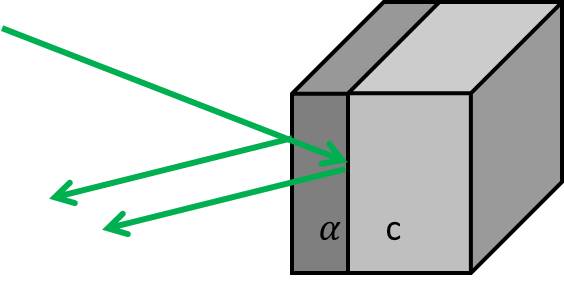
Consider the case that the amorphous layer is on the top of the crystalline layer. If the laser beam is perpendicular to the surface, a portion of the beam will be reflected from the outer surface and others penetrate and reflected from the a/c interface due to the discontinuity of refraction index at the boundary. If the optical constants of layers are known, the reflectivity to time measurement can be converted to depth to time, z(t), straightforwardly. The theoretical reflectivity as a function of depth can be expressed as
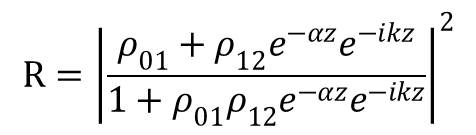
In this expression, z is the thickness of amorphous layer, ρ01=(1-n1)/(1+n1 ) and ρ12=(n1-n2)/(n1+n2) are the reflection coefficients at the air/a interface and a/c interface, where n1 and n2 are the complex indices of refraction of a-Si and c-Si, respectively. The wave number and absorption coefficient are also presented in this expression as k=(2π/λ)Re(n1 ) and α=(4π/λ)Im(n1 ).
The theoretical reflectivity versus amorphous layer thickness with 532nm laser can be calculated and plotted as
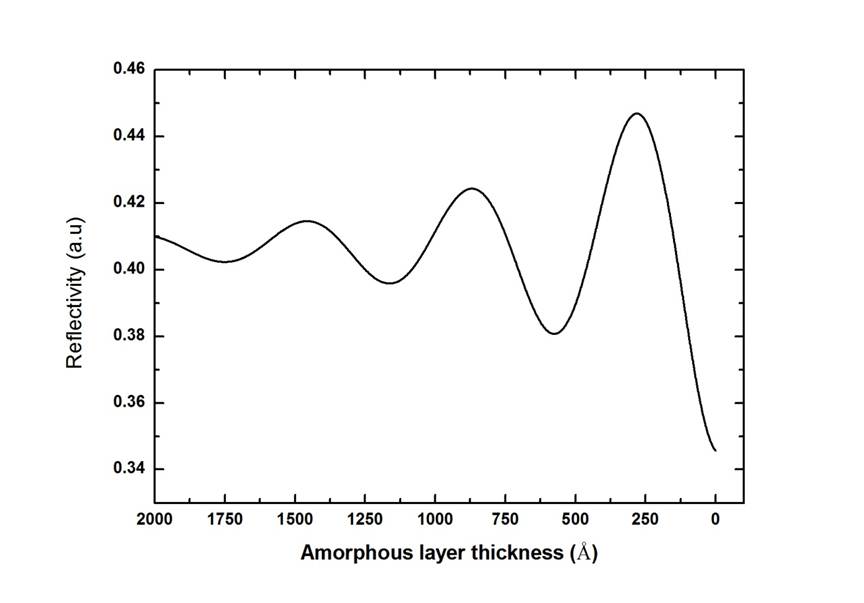
The gradually reduced amplitude of reflectivity oscillations is due to absorption in amorphous layer and attenuated the intensity reflected from a/c interface. Consequently, the detectable and suitable SPER dynamic measurement range will be reduced to the depth within 2000 angstrom from the surface.
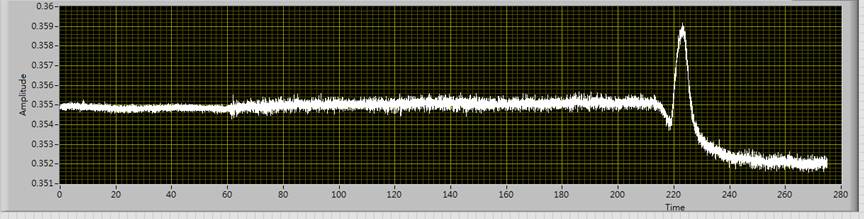
Figure shown below is the typical experimental signal we get from the TRR-RTA system, with further calculation, Since the depth to time are converted, the SPER rate as a function of depth can be generated from differentiating z(t). With the calculated regrowth rate we can analysis the kinetic of SPER.
© 中央大學凝態物理實驗室 Condensed Matter Physics Laboratory, National Central University
320 桃園縣中壢市中大路300號 No.300, Jhongda Rd., Jhongli City, Taoyuan County 32001, Taiwan(R.O.C.)
Tel: 886-3-4227151ext.65399 | Email: wywoon@phy.ncu.edu.tw